Die Finanzmathematik
(Rosa Golluscio)
Kaum ein anderes mathematisches Gebiet hat sich in den letzten Jahrzehnten so stark weiterentwickelt wie die Finanzmathematik. Ihre wichtige Bedeutung wird z.B. durch die zwei Wirtschaftsnobelpreise verstärkt, die zum einen Markowitz 1990 für seine Portfoliotheorie und zum anderen Merton und Scholes für die Bewertung derivater Finanzinstrumente erhielten. In diesem mathematischen Bereich ist das Hauptziel, Erschlüsse über Modelle und Prozeduren herauszufinden, die vor allem im Bankwesen und in der Wirtschaft eine große Rolle spielen.
Das zentrale Problem der Finanzmathematik besteht in der Bewertung von Zahlungen, seien es zukünftige oder vergangene. Die klassischen Themen der Finanzmathematik beschäftigen sich mit der Diskontierung, mit der Kalkulation von Auszahlungs- und Tilgungsplänen und der Zinsberechnung, aber auch mit den Anwendungen in der betrieblichen Investitionsrechnung. Dabei greift sie auf Techniken und Ergebnisse der Algebra, Analysis und der Wahrscheinlichkeitstheorie zurück.
1) Diskontierung:
Die Aufgabe zu einem späteren Zeitwert denjenigen
Anfangswert(Barwert) zu errechnen, der durch Verzinsung auf den gegebenen
Zeitwert anwachsen wird.
Diskontierung werden also zum Vergleich von “Zahlungen heute“ mit “Zahlungen morgen“ genutzt. Die Berechnung des heutigen Barwerts (present value) ermöglichen verschiedene Diskontfunktionen d(t).
=> Problem: Wie viel ist eine nach n Jahren sicher fällige Geldeinheit heute wert?
Voraussetzung:
Einkommensströme, die genau bekannt sind, wie z.B. nicht kündbare Obligationen
Bedingung:
1) d(0) = 1
2) d(t) ist streng monoton fallend; t Jahre(t =0,1,2,...,n)
3) lim d(t) = 0 (Je weiter in der Zukunft eine Zahlung erfolgen soll, desto geringer ist ihr heutiger Wert)

d(t) kann beliebig verlaufen
Es gibt 3 einfache Diskontfunktionen:(i=Zinssatz, k=Anzahl der Zeiteinheiten)
- Amtliche Diskontfunktion
![]()
- Kaufmännische Diskontfunktion
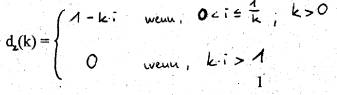
- Geometrische Diskontfunktion
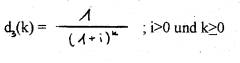
2) Zinsbegriff:
Der Zins(lat.:census=Abgabe) ist der Preis für die zeitweilige
Überlassung von Geld. Der Zinsbegriff steht in enger Verwandtschaft mit der
Diskontfunktion, da sie die Inverse zu den einfachen Diskontfunktionen bilden.
=> Problem: Wie
viel ist eine heute ausgeliehene Geldeinheit in n Jahren wert?
- Einfache Verzinsung (Inverse
Funktion zur amtlichen Diskontierung)
Definition:
Jahreszinsen immer gleich groß, denn sie sind immer vom ursprünglichen
Kapital K0(Anfangskapital) zu berechnen, wobei i der Zinssatz ist.
Endkapital am Ende des 1.Jahres:K1= K0+K0*i = K0(1+i)
Endkapital am Ende des 2.Jahres: K2= K0+K0*i+K0*i = K0(1+2i)
Kn = K0(1+ni)
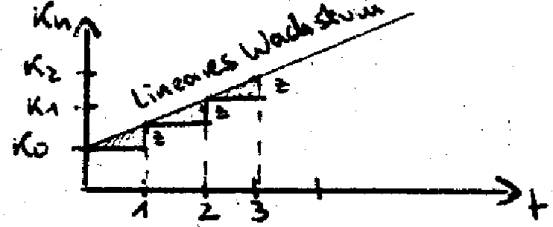
Jährlicher Zuwachs z immer gleich
=> z= K0*i
- Geometrische Verzinsung (inverse Funktion zur geometrischen Diskontierung)
Definition:
Bei dieser Verzinsung werden Kapital und Zins am Ende jeder Zeiteinheit
als neues Kapital aufgefasst, welches wiederum zum gleichen Zinssatz für die
nächste Zeiteinheit reinvestiert wird (Zinseszins). Diesen Vorgang nennt
man Aufzinsung.
Hier spielt vor allem die geometrische Reihe eine große Rolle, da auch
dort der Quotient konstant bleibt.
Endkapital am Ende des 1.Jahres: K1=K0+K0*i= K0(1+i)
Endkapital am Ende des 2.Jahres: K2=K1+K1*i= K1(1+i)= K0(1+i)(1+i)=
K0(1+i)2
Kn = K0(1+i)n Aufzinsungsfaktor q =(1+i), n =Anzahl der
Jahre

- Gemischte Verzinsung
Definition:
Die Verzinsungszeit n wird durch ganze Zahlen von Jahren N und dem Teil
t eines Jahres gegeben(z.B. n= von 15.9.58 bis 20.9.65 => N=6 und t=260)
Kn = K0*(1+ti)N
3) Rente
Rente im engeren Sinne, also ein in gleichen Zeitabständen und in gleichenbleibender Höhe verlaufender Prozess, wird als Cashflow bezeichnet, der in regelmäßigen Zeitabständen verläuft. Dabei ist die monatliche Rente bzw. jährlich Rente jener Betrag, den man monatlich bzw. jährlich als Zusatzeinkommen erwarten kann.
Man unterscheidet zwei Arten von Rentenauszahlungen:
Nachschüssige Rentenzahlung
(hier erfolgt die erste Zahlung eine Zeitperiode nach Rentenbeginn und die letzte bei Rentenende)

Barwert der Einheitsrente
![]()
Endwert der Einheitsrente
![]()
Vorschüssige Rentenzahlung
(hier erfolgt die erste Zahlung bereits bei Rentenbeginn und die letzte eine Zeitperiode vor Rentenende)
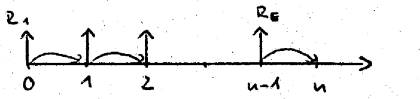
Barwert der Einheitsrente (Wert zum heutigen Zeitpunkt)
![]()
Endwert der Einheitsrente
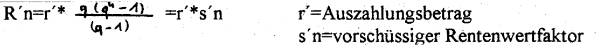
Erbrentenproblem:
Bekanntlich basieren Altersrenten auf einer Solidarität aller
versicherten. Die, die aber zu früh sterben und daher keine Leistungen
beziehen, finanzieren die Renten die länger als erwartet leben, wobei die Erben
bei dieser Rentenform leer ausgehen. Um diesen Mangel zu beheben, schließt man
einen Erbrentenvertrag ab, bei dem die Erben bei frühzeitigen Tod die Rente
erhalten. Obwohl die Erbrente eine feste Laufzeit besitzt und sie daher mit der
finanzmathematischen Definition einer Rente übereinstimmt, gehört diese
Rentenform doch mehr zur Lebensversicherungsmathematik.
4) Schulden und Schuldentilgung:
Schulden unterscheidet man nach ihrer wirtschaftlichen Form und ihren
Rückzahlungsmerkmalen:
- Gesamtfällige Schuld, Anleihe (Rückzahlung in einem Betrag)
- Ewige Rente, Aktien (keine Rückzahlung)
- Tilgungsschulden z.B. Hypotheken (Rückzahlung in Teilbeträgen)
Die Rückzahlung bei Tilgungsschulden(z.B. Hypotheken, Anleihen) enthält
nicht nur die anfallenden Zinsen, sondern auch den Tilgungsbetrag.
Tilgung: T= Annuität(das was man am Ende eines Jahres zahlen muss)- Zinsen von Gesamtschuld
Restschuld Km nach m Jahren:
Km= K0-(T1+T2+...+Tm)
Tilgungsplan
|
Jahr |
Schuld am Anfang eines Jahres |
Zinsbetrag am Ende des Jahres |
Zinsersparnis gegenüber Vorjahr |
Tilgungsrate am Ende eines Jahres |
|
1 |
K0 |
Z1 |
0 |
T1=A-K0*i |
|
2 |
K1=K0-T1 |
Z2=Z1-T1*i |
T1*i |
T2=T1+T1*i=T1(1+i) |
|
... |
... |
... |
... |
... |
|
m |
K(m-i)=K(m-2) -T(m-1) |
Zm=Z(m-1)-T(m-1)*i |
|
Tm=T1(1+i)hoch(m-1) |
5) Kursberechnung von Aktien und ihre Bewertung:
Berechnung:
|
Nominelle Ebene (Vertragsgröße),
in der das Nominalkapital und der nominelle Zinssatz (coupon j) angegeben
werden. |
![]() Kurs C(t)=(100*
(Nominalkapital/Realkapital) )%
Kurs C(t)=(100*
(Nominalkapital/Realkapital) )%
|
Reale Ebene (Marktbewertung
der Vertragsgröße), in der der reale Wert (Barwert oder Rendite) angegeben
wird. |
Quellen:
www..mathematik.uni-kl.de/mathint/finmat/fin_math.htm
„Einführung in die Finanzmathematik“, Bühlmann,1992