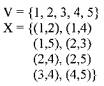
Unter einem Graphen versteht man eine zeichnerische Konstruktion, die zum einen aus einer Menge von Punkten (Knoten) besteht, zum anderen aus speziellen Geraden (Kanten), die diese Punkte untereinander verbinden.
 

Definition: Ein Graph G besteht aus einer endlichen Menge V von n Knoten zusammen mit einer gewissen Menge X von m zweiwertigen Teilmengen von V.

Beispiel:
 

Bild 0a: Das Haus vom Nikolaus	Bild 0b:Ein zugehöriger Graph

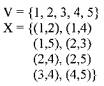Jeder Graph ist nur im Hinblick auf seine strukturellen Aspekte interessant. Entscheidend ist, dass er die Beziehungen der einzelnen Knoten zueinander hervorhebt. Die Gestaltung ist dabei zweitrangig. Häufig kann er auch auf mehrere verschiedene Arten gezeichnet werden.

Sinn und Zweck der Graphentheorie ist es nun, unterschiedliche Probleme aus vielen verschiedenen Bereichen auf Graphen hin zu formulieren und anhand dieser Veranschaulichung und mit Hilfe bestimmter Rechenmethoden diese zu lösen.
 
 

2. Geschichte der Graphentheorie

Der erste, der historisch gesehen die früheste graphentheoretische Abhandlung schrieb, war Leonhard Euler (1707-1783). Mit seinem Werk solutio problematis ad geometriam situs pertinens (dt: Problemlösung bezüglich einer geometrischen Lage) aus dem Jahre 1736, zu dem er durch das Königsberger Brückenproblem angeregt wurde (s. 1. Bsp.), leistete er den ersten Beitrag zur Graphentheorie und gilt folglich als ihr Begründer. Außerdem stellte er die Formel n+l = m+2 (n = Ecken, l = Flächen, m = Kanten) auf, die für jedes Polyeder gilt. Sie ist heutzutage wichtiger Bestandteil der Graphentheorie und nimmt einen entscheidenden Platz in der Theorie der planaren Größen ein. Trotz dieser wegweisenden Veröffentlichungen folgte in den nächsten 100 Jahren keine weitere systematische Beschäftigung mit Graphen.

Einen erneuten Anstoß erhielt die Graphentheorie von den im 19. Jahrhundert sich schnell entfalteten Naturwissenschaften. Insbesondere Gustav Robert Kirchhoff (1824-1887) trug mit einer grundlegenden Arbeit über elektrische Ströme und Spannungen dazu bei. Auch der Ursprung der heute so bedeutungsvollen Netzwerktheorie, in der es hauptsächlich um Verkehrs- und Transportprobleme (s. 2. Bsp.) geht, findet sich in seinem Werk wieder.

Über die Chemie gelangte Arthur Cayley (1821-1895) zur graphentheoretischen Struktur. Indem er die Anzahl isomerer Alkane mit gleicher Summenformel untersuchte, entwickelte er eine systematische Methode zur Anzahlbestimmung von Isomeren und schuf damit die mathematische Grundlage für eine allgemeine Abzählungstheorie. Außerdem stellte er als erster das sogenannte Vierfarbenproblem (s. 3. Bsp.) dar, das über 100 Jahre lang die Entwicklung der Graphentheorie äußerst fruchtbar beeinflusst hat.

Durch die rasanten Fortschritte in der Computertechnik nach 1945 erhielt die Graphentheorie neue Impulse. Viele Optimierungsaufgaben mit ökologischen Hintergrund konnten von nun an mit ihrer Hilfe gelöst werden (s. 4. Bsp.).

Insgesamt hat sich die Graphentheorie sehr sprunghaft und vor allem in den letzten 40 Jahren stark entwickelt. Heute nimmt sie einen zentralen Platz in der angewandten Mathematik ein.
 

3. Anwendungen der Graphentheorie

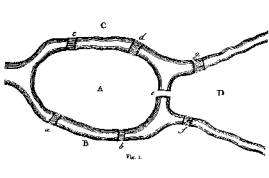
1. Beispiel:  Das Königsberger Brückenproblem

	Bild 1a: Skizze aus L. Eulers Werken		Bild 1b: Ein zugehöriger Graph

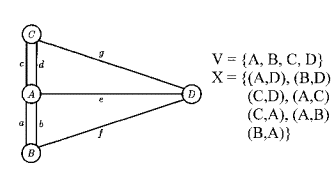
Anhand der Lageskizze kann ein Graph erstellt werden. Die Insel A und die Ufer B, C, und D werden zu Knoten, die Brücken a, b, c, d, e, und f bilden die Kanten des Graphen.

Der gesuchte Rundgang entspricht einem geschlossenen Weg, der die Eigenschaft haben muss, jede Kante genau einmal zu enthalten (= Eulerscher Kreis). Der Gegensatz dazu wäre ein geschlossener Weg, der jeden Knoten genau einmal enthält (= Hamiltonscher Kreis).

Ein Eulerscher Kreis ist in diesem Beispiel nicht möglich. Dies zeigt uns der Eulersche Satz:
 
 

d(A) = 5; d(B) = d(C) = d(D) = 3   =>  Es gibt keinen solchen Rundgang in Königsberg.

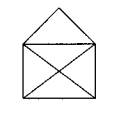
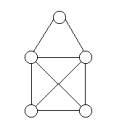
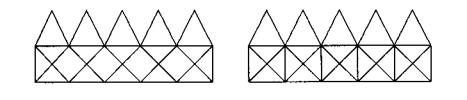
Auf demselben Satz basiert auch der Grundgedanke des Hauses vom Nikolaus: =>  d(untere Ecken) = 3; d(obere Ecken) = 4; d(Spitze) = 2   =>  Wenn die unteren Ecken als Anfang und Ende genommen werden, lässt sich das Haus in einem Zug zeichnen.

Aufgabe: Welches der folgenden beiden Nikolausreihenhäuser kann man mit einem Zug zeichnen? Begründung!
 

Bild 1c: Reihenhaus I vom Nikolaus                     Bild1d: Reihenhaus II vom Nikolaus

2. Beispiel:  Maximalflussproblem

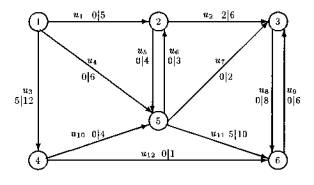
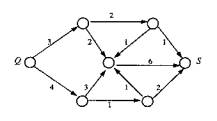
Eine Speditionsfirma will ein Gut über eine weite Strecke von einer Stadt (1) in eine andere Stadt (6) transportieren, wobei an 4 Verladungsorten (2, 3, 4 und 5) umgeladen werden kann. Diese 6 Städte bilden die Knoten, die 12 nur in einer Richtung zu befahrenden Verbindungen die Bögen des zugehörigen gerichteten Graphen.

1. Voraussetzung: An den Knoten 2, 3, 4, und 5, an denen umgeladen werden kann, muss die einfließende Menge der Güter mit der ausfließenden Menge übereinstimmen (= Knotenregel)

2. Voraussetzung: Die über die Bögen u_k transportierte Menge, die man als Flusswert f(u_k) misst, muss zwischen einer unteren Schranke a_k und einer oberen Schranke b_k liegen (s. Bild 2a: a_k|b_k): a_k kleiner oder gleich f(u_k) kleiner oder gleich b_k

Frage: Was ist die größtmögliche Menge (= Maximalfluss), die von 1 nach 6 transportiert werden kann?
 
 

Bild 2a: Beispiel zum Maximalflussproblem	Bild 2b: Graph zur Aufgabe

1. Weg (u1, u2, u8): f(u1) = f(u2) = f(u8) = 5 => a2 nicht unterschritten => ß1, ß2 und ß8 nicht überschritten	2. Weg (u3, u12): f(u3) = f(u12) = 1 => a3 bis jetzt unterschritten => ß3 und ß12 nicht überschritten
3. Weg (u3, u10, u11): f(u3) = f(u10) = f(u11) = 4 => a3 jetzt nicht mehr unterschritten => a11 bis jetzt unterschritten => ß3, ß10 und ß11 nicht überschritten	4. Weg (u4, u11): f(u4) = f(u11) = 6 => a11 jetzt nicht mehr unterschritten => ß4 und ß11 nicht überschritten

Es können somit 5+1+4+6 = 16 Güter transportiert werden. Dies ist die maximale Anzahl, da das Ziehen einer Trennlinie durch u1, u4, u10 und u12 ergibt: a1+ a4+ a10+a4 = 16
Aufgabe: Wie viele Güter können maximal von Q nach S transportiert werden (s. Bild 2b)?
Welche Bögen sind die Engpässe?

3. Beispiel: Vierfarbenproblem
Frage: Ist es möglich, die Länder einer jeden Landkarte mit höchstens 4 verschiedenen Farben zu färben, so dass benachbarte Länder stets unterschiedlich gefärbt sind? 

Bild 3a: Kartenskizze	Bild 3b: Ein zugehöriger Graph

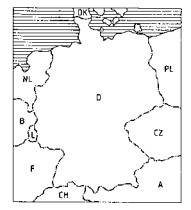
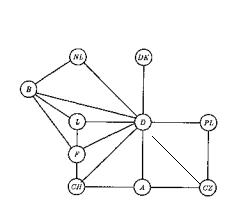
Diese Frage beschäftigte Mathematiker über ein Jahrhundert lang, ehe vor ungefähr 10 Jahren bewiesen werden konnte, dass es möglich ist. Der Beweis dazu ist äußerst kompliziert und umfasst mehrere hundert Seiten. Anhand der graphischen Anschauung der Lage Deutschlands kann dies bestätigt werden: Die Länder A, B, CH, (ehem.) CZ, D, DK, F, L(UX), NL und PL sind die Knoten des Graphen, die Grenze zwischen zwei benachbarten Ländern die Kanten.
Wegen der Lage von B, D, F und L, bei denen jedes Land zum anderen eine Grenze hat, sind 4 Farben notwendig. Diese sind insgesamt ausreichend, wie folgendes Beispiel zeigt:
CZ, DK, F, NL: = rot         A, L, PL: = blau         B, CH: = grün         D: = gelb
 

4. Beispiel:  travelling salesman problem

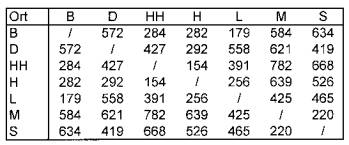
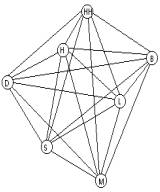
Ein Handelsreisender will eine Rundreise (= Tour) durch n Städte organisieren, wobei er die Entfernungen zwischen den Städten kennt. Er sucht die Rundreise mit der kleinsten Gesamtlänge (= optimale Tour). Diese soll nun durch Deutschland gehen und die Städte München (M), Stuttgart (S), Leipzig (L), Hannover (H), Düsseldorf (D), Hamburg (HH) und Berlin (B) umfassen (n = 7).
 
 

Tabelle 4a: Entfernungen der einzelnen Städte in km	Bild 4b: Beispiel zum travelling salesman problem

Der zugehörige Graph besteht aus (n-1)+(n-2)+(n-3)+(n-4)+(n-5)+(n-6) = n(n-1)/2 = 21 Kanten und n = 7 Knoten. Da dies die Höchstzahl aller möglichen Kanten ist, heißt der Graph vollständig. Diese Graphen sind häufig unübersichtlich.
Gesucht ist nun der kürzeste geschlossene Weg, der jeden Knoten genau einmal enthält (= Hamiltonscher Kreis). Die Anzahl der Hamiltonschen Kreise errechnet sich wie folgt:
Man nummeriert die Knoten von 1 bis n und stellt jeden Hamiltonschen Kreis durch einen n-Tupel dar: (i₁, i₂, i₃, i₄, i₅, i₆, i₇)
=>   i₁ = 1, da der Ausgangspunkt der Tour egal ist
=>  Die restlichen Knotennummern lassen sich auf (n-1)! verschiedene Weisen anordnen
=>  (n-1)!/2, da es auf die Richtung der Rundreise nicht ankommt

Folglich gibt es (n-1)!/2 = 6!/2 = 360 solcher Hamiltonscher Kreise. Mit Hilfe der einzelnen Entfernungen (s. Tabelle 4a) kann man nun die optimale Tour ausrechnen. Sie wäre in diesem Fall B-HH-H-H-D-S-M-L-B mit einer Länge von 1973 km.

=>  Dieses Vorgehen ist aber nicht sehr praktikabel, da die Anzahl der Hamiltonschen Kreise mit zunehmenden n exponentiell wächst

=>  In der Graphentheorie gibt es ein Nährungsverfahren, das viel weniger Aufwand erfordet
 
 

Zusammenfassung der Anwendungen:

- Viele alltägliche Probleme können durch die Veranschaulichung anhand eines Graphen präzisiert und gelöst werden

- Graphen stellen geeignete Objekte der Komplexitätslehre dar (= Forschungsbereich der Mathematik, der versucht, das gleiche Problem mit einfacheren Rechenschritten zu lösen)

- Anwendung der Graphentheorie auf Bäume mit Wurzeln, z. B. bei Stammbäumen von Königshäusern oder Rennpferden

- Häufige Verwendung bei Optimierungsaufgaben mit ökonomischen Hintergrund, z. B. bei Abstands- und Stromproblemen oder im selbstständigen Gebiet der Netzplantechnik (= Bestandteil des Projektmanagements: zur Modelbildung bei der Planung von Prozessabläufen)
 
 

4. Quellen

Diestel, Reinhard (1996). Graphentheorie. Berlin, Heidelberg: Springer Verlag

Nägler, Günter; Stopp, Friedmar (1996). Mathematik für Ingenieure und Naturwissenschaftler. Graphen und Anwendungen. Stuttgart, Leipzig: B. G. Teubner Verlagsgesellschaft

Volkmann, Lutz (1991). Graphen und Digraphen. Eine Einführung in die Graphentheorie. Wien, N. York: Springer Verlag

Volkmann, Lutz (1996). Fundamente der Graphentheorie. Wien, New York: Springer Verlag