Kryptographie

(Katharina Deuse)

Griech.: Krypto ( ich verberge ) und graphe ( das Schriftstück )

Kryptographie (=Verschlüsselung) wird mit Krypotanalyse (=Entschlüsselung) unter dem Überbegriff Kryptologie zusammengefasst.

Einsatzgebiete der Kryptographie

- sensible Daten in der Wissenschaft

- Abwicklung von Geschäftsvorgängen

- Vertrauliche Informationen im Privatleben

Ziele der Kryptographie

- Vertraulichkeit: Schutz vor fremden Augen

- Integrität: Schutz vor Manipulation

- Authentizität: Schutz vor falschen Absendern

Kombination aller drei Ziele zur Gewährleistung der bestmöglichsten/sichersten Verschlüsselung

Erklärungen:

Schlüssel: Parameter, der bei Verschlüsselung in die Operationen einfließt und das Ergebnis wesentlich verändert

Symmetrisches Verfahren: Schlüssel und Gegenschlüssel sind identisch

Asymmetrisches Verfahren: Schlüssel und Gegenschlüssel unterscheiden sich

Konfusion: Verschleierung des Zusammenhangs zwischen Klartext und Geheimtext mit einfachen Regeln

Diffusion: Regelmäßigkeiten in den Klartextzeichen werden über mehrere Zeichen hinweg verteilt, so dass sie schwerer aufzufinden sind

Beispiel:

2 0 . 0 8 . 9 9 2 1 . 0 8. 9 9

KLM9G3AM KGM9G3AM (Konfusion, „08.99“ entspricht jeweils der gleichen Zeichenfolge)

R 2D 208 1 5 4 7 11C3 PO (Diffusion)

Kryptographische Verfahren zur Gewährleistung von Vertraulichkeit

Symmetrische Verfahren mit Hilfe von Konfusion

- Spiegelschrift

- Caesar-Chiffrierung:

Verschiebung des lat. Alphabets um z.B. 3 Stellen nach rechts (hier: Zahl „3“ bzw. „C“ ist der Schlüssel)

Vorteile: Schlüssel ist kurz und leicht zu merken bzw. zu übertragen, Verschiebung ist leicht zu berechnen

Nachteile: Schlüsselübermittlung muss geheim erfolgen; wenig Schlüssel => schnelle und leichte Möglichkeit alle Schlüssel durchzuprobieren; Buchstabenhäufigkeit

- Vigenère-Verschlüsselung

Polyalphabetische Verschlüsselung, d.h. ein Wort (hier: TAPIR) wird als Schlüssel eingefügt und das Alphabet wird jeweils umsortiert.

O R E I L L Y I S T S P I T Z E Originaltext

T A P I R T A P I R T A P I R T Schlüsselwort

20 1 16 9 18 20 1 16 9 18 20 1 16 9 18 20 zur jeweiligen Caesar-Chiffrierung gehörende Zahl

I S U R D F Z Y B L M Q Y C R Y Verschlüsselter Text

- Die Enigma

Mehrere Rotorscheiben hintereinander, die mit unterschiedlicher “Schlüsselzahl” rotiert werden; Ergebnis ist entscheidend

Vorteile: bei 3 Rotorscheiben schon 26³ = 17.576 Schlüsselmöglichkeiten

- One-Time-Pad

Jeder Schlüssel wird nur einmal verwendet

- große Mengen von Schlüsseln werden gebraucht

Symmetrische Verfahren mit Hilfe der Diffusion

Feistel – Netzwerke

Eingabeblock und Schlüssel in mehrere kleine Blöcke eingeteilt; Operationen der Verschlüsselung werden auf die einzelnen Eingabeblöcke angewendet und später durch XOR miteinander verknüpft; 16 solcher Runden werden ausgeführt

DES > Eingabeblock in 2 Hälften, Schlüssellänge von nur 64 Bytes (>Sicherheit zu gering) =>

Triple DES > 2 Schlüssel zu je 56 Bytes; Text wird zuerst mit dem ersten Schlüssel verschlüsselt, dann nocheinmal mit dem zweiten => mehr Sicherheit

IDEA > Eingabeblock zuerst in Blöcke von 64 Bytes, dann in 4 Teilstücke zu 16 Bytes eingeteilt; Schlüsselbits (Länge 128 Bit) in 52 Teilschlüssel zu 16 Bit eingeteilt => Sicherheit

BLOWFISH > Blöcke mit 64 Bit Länge, Schlüssel mit beliebiger Länge bis zu 448 Bit => schnelles und sicheres Verfahren

AES > symmetr. Blockverschlüsselung mit 128 Bytes Blocklänge und 128, 192 und 256 Bit Schlüssellänge

Nachteile symmetrischer Verfahren:

- Schwierigkeit für Kommunikationspartner Schlüssel miteinander auszumachen

- Angreifer können falsche Schlüssel unterschieben

- Starr gegen Modifikationen => bei erhöhtem Sicherheitsbedarf wird aufwendige Neuentwicklung nötig

Asymmetrische Verfahren (Diffusion) / Public - Key - Verfahren

Ein Kommunikationspartner wählt ein Schlüsselpaar aus (enge formelmäßige Beziehung zw. beiden Schlüsseln); einer der Schlüssel wird veröffentlicht ( > Public – Key) = Verschlüsselung der Texte; der andere wird einbehalten als Geheimschlüssel zur Entschlüsselung der Geheimtexte

- nur noch ein Schlüsselpaar nötig

- keine Möglichkeit für Fremde mitzulesen, da Geheimschlüssel zur Entschlüsselung nötig

- Verfahren zu komplex, um den Geheimschlüssel nachzurechnen/auszurechnen

RSA (Primzahlen- und Restklassenalgorithmus)

Zufällig zwei Primzahlen auswählen z..B. p = 29 , q = 37 ; nur werden n = p q = 1073 und r = (p – 1) (q – 1) berechnet; beliebige Zahl e , die zu r teilerfremd ist auswählen, z.B. e = 17;

e und n sind die öffentlichen Schlüssel; d (geheimer Schlüssel) = e modulo r mit Rest 1;

p , q , r werden nicht mehr gebraucht > müssen gelöscht werden, da sonst d berechnet werden kann.

Verschlüsselung:

424 711 081 520 081 965

---- . ---- . ---- . ---- . ---- . ---- => m_i ^e modulo n = Rest

m₁ m₂ m₃ m₄ m₅ m₆

Entschlüsselung:

Rest_i ^d modulo n = Rest = m_i

Rest_i ^d

--------- => Rest = m_i

N

El Gamal (Primzahlen- und Restklassenalgorithmus)

y = g ^x modulo p g (gegebene Basis) zufällig ausgewählt

p (selbst ausgesuchte Primzahl); so gewählt, dass auch (p – 1)/2 prim

y, x (gesucht); x muss geheim gehalten werden/zufällig ausgewählt

g, y, x natürliche Zahlen zwischen 1 und p – 1

p, g, y öffentlicher Schlüssel

=> diskreter Logarithmus

Verschlüsselung:

Blockeinteilung m_i (wenn Nachricht größer als p ); Absender wählt beliebige Zahl k , teilerfremd zu p – 1, berechnet die Werte a = g ^k modulo p und b = y ^k ∙ m_i modulo p und sendet Geheimtext an Empfänger; k löschen, da sonst aus b, y, k m konstruiert werden kann

Entschlüsselung:

b

--------------------- modulo m_i = Klartext

a ^x modulo m_i

Vorteile (Public - Key - Verfahren):

- genug Primzahlen

- ein einziges Schlüsselpaar

- Unmöglichkeit, aus Geheimtext ohne Geheimschlüssel Klartext abzuleiten

- Skalierbarkeit (bei Fortschritt durch schnellere Computer, Möglichkeit größere Schlüssel zu entwerfen)

Nachteile (Public - Key - Verfahren):

- Geheimtext wesentlich länger als Klartext

- Berechnungen Sehr zeitaufwändig

- Veröffentlichten Schlüssel zurückzurufen schwierig, da öffentlicher Schlüssel überall gespeichert

- Möglichkeit der Listenerstellung bei zu kurzen Nachrichten

Hybridsysteme (Kombination der Stärken beider Arten von Systemen, z.B. RSA und IDEA)

Empfänger erzeugt Schlüsselpaar und gibt den öffentlichen Schlüssel bekannt; Absender kodiert Klartext mit zufällig erzeugtem IDEA - Schlüssel (=Sitzungsschlüssel), kodiert dann Sitzungsschlüssel mit öffentlichem RSA - Schlüssel und schickt Geheimtext an Empfänger

Vorteile:

- Public – Key – Verfahren stellt abhörsicheren Kanal, auf dem Schlüssel des symmetrischen Verfahrens ausgetauscht werden kann, zur Verfügung

- Schnellere Übertragung Keine Struktur im Sitzungsschlüssel => kaum Angriff möglich

Nachteil:

- Komplexität des Gesamtsystems deutlich höher

Verschiedene Betriebsarten der Verschlüsselungsmethoden

- Electric Codebook (ECB):

Jeder Block wird unabhängig verschlüsselt und am Ende mit den ansderen verknüpft

- Cipher - Block - Chaining (CBC):

Mitlesen und Block - Replay - Angriff durch Verkettung des Geheimtextes mit dem Klartext erschwert;Wiederholungen im Klartext sollen im Geheimtext vermieden werden

- Komprimierung:

Wiederholungen im Klartext lassen sich durch Komprimierung vor der Verschlüsselung vermindern => verringerte Datenmenge lässt sich schneller verschlüsseln und übertragen

Kryptographisches Verfahren zur Sicherstellung von Integrität

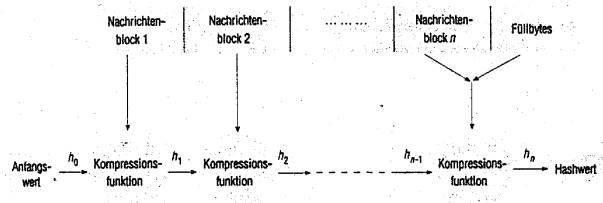
Hashfunktion

Prüfsummen (XOR – Wert aller Bytes) werden berechnet, an das Datenpaket angeschlossen und übermittelt; empfangendes Programm führt dieselbe Berechnung aus; Übereinstimmung => mit hoher Wahrscheinlichkeit korrekt übertragen; keine Übereinstimmung => fehlerhaft; Lange der Nachricht muß in den Hashwert miteingebaut werden, damit Angreifer den Text in der Länge nicht zu verändern können, so daß gleicher Hashwert und sinnvoller Text mit anderer Länge herauskommen

Vorteil:

- Prüfsummen (Message Digits) für beliebig lange Nachrichten einfach und schnell berechenbar

- Stets kurze Zahl fester Länge um Zeitaufwand bei Übermittlung gering zu halten

- für jedermann leicht zu berechnen

- praktisch ausgeschlossen für vorgegebenen Hashwert Nachricht mit gleichem Hashwert zu konstruieren

Nachteile:

- Kollisionsgefahr (Paare von Nachrichten mit gleichem Hashwert)

- Prüfsummen müssen über anderes Medium übermittelt werden

Kryptograhische Verfahren zur Sicherstellung von Authentizität

MAC’s (Message Authentication Codes)

Absender berechnet Hashwert der Nachricht und lässt den geheimen Schlüssel miteinfliessen => Angreifer kann Nachricht nicht so lang weitermodifizieren, bis gleicher Hashwert herauskommt, weil er den geheimen Schlüssel und damit den Hashwert des Blocks mit dem Schlüssel nicht kennt.

Vorteil:

Kein Dritter kann Nachricht fälschen

Nachteil:

Absender kann jederzeit behaupten, das Dokument sei vom Empfänger erstellt

Signaturen

- Trust Center mit Funktion eines Notars zwischen geschaltet

Alice vereinbart Schlüssel mit Trust Center (nur TCT und Alice bekannt), verschlüsselt Nachricht mit Schlüssel und schickt Geheimtext an Trust Center; TC entschlüsselt Nachricht, verschlüsselt sie wieder mit Schlüssel, der mit Bob ausgemacht würde und schickt sie zussammen mit Geheimtext von Alice an Bob; Bob entschlüsselt Geheimtext und speichert Alices Geheimtext (als Beweis, da er damit nichts anfangen kann)

=> Teuer wegen Kosten für Verschlüsselung und für Gewährleistung der Sicherheit

- Public – Key – Verfahren

Alice verschlüsselt mit eigenem geheimen Schlüssel und schickt Geheimtext an Bob; dieser entschlüsselt Nachricht mit Alices öffentlichem Schlüssel => Authentizität gesichert

- Hashverfahren

Alice berechnet Hashwert der Nachricht, verschlüsselt diesen mit eigenen geheimen Schlüssel und schickt ihn zusammen mit Nachricht an Bob => Authentizität / Integrität gesichert

Kombination von Vertraulichkeit, Integrität und Authentizität

Quelle: Kryptographie, Gisbert W. Selke