Kugelpackungen
(Ursula Koebele)
Im Alltag begegnen uns Kugelpackungen
sehr oft. Orangen kauft man meist netzförmig verpackt. Eine solche
Packung kann als einfaches Modell einer clusterförmigen Packung dienen.
Tennisbälle dagegen werden in der Regel stangenförmig verpackt,
sie stellen ein Modell einer wurstförmigen Packung von dreidimensionalen
Kugeln dar.
Cluster- und wurstförmige
Kugelpackungen zählen zu Packungen von endlicher Stückzahl (finite
Packungen). Im Gegensatz dazu beschreiben infinite Packungen eine unendliche
Anzahl von gepackten Kugeln (annähernd: Goldoberfläche, Edelgase,
NaCl, Diamanten,...).
Gitter
Im 2-dimensiünalen Raum
ist ein Gitter eine regelmäßige Anordnung von Punkten m einer
Ebene. Für eine ebene Ausdehnung benötigt man zwei Vektoren a
und b (fett geschriebene Buchstaben sollen Vektoren symbolisieren),
die nicht linear abhängig sind. Die von a und b erzeugte
regelmäßige Anordnung wird zweidimensionales (Punkt-)Gitter
genannt.
Definition: a
und b seien Vektoren in der Ebene IR2; a nicht
0,
b
nicht 0, a nicht parallel b, dann heißt die
Menge G = { ma + nb : m, n aus Z} ein zweidimensionales
Gitter und { a, b} eine Basis.
Ein Gitter ist also die Menge aller ganzzahligen Linearkombinationen
der beiden Basisvektoren.
Bei einem dreidimensionalen Gitter kommt zu den Vektoren a und
b
ein dritter Vektor c.
Definition: a, b und c seien Vektoren im Raum
IR3, c nicht gleich la + mb für irgendein l
und m, analog für a und b. Dann heißt die Menge G ={ la
+ rnb + nc | l. m, n aus Z } ein dreidimensionales Gitter, {a,
b, c} eine Basis.
Allgemein:
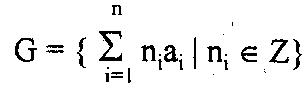
Fundamentalparallelotop Ein Fundamentalparallelotop ist der
Körper, der von den Basisvektoren aufgespannt wird. Im IR2 handelt
es sich dabei um ein Parallelogramm, im IR3 um einen Spat.
Zu einem bestimmten Gitter gibt es verschiedene Basen. Die von Basen aufgespannten
Parallelogramme besitzen den gleichen Flächeninhalt, von Nichtbasen aufgespannte
Parallelogramme weisen "echte" Vielfache des Flächeninhalts auf.
Definition: G sei ein n-dimensionales Gitter und {a1,
a2, ..., an} eine Basis von G, dann heißt
sein Fundamentalparallelotop. Satz: alle möglichen, verschiedenen
Fundamentalparallelotope eines Gitters haben das gleiche Volumen. (Beispiele
auf Folie)
Infinite Kugelgitterpackungen
Eine infinite Kugelgitterpackung besteht aus einem n-dimensionalem Gitter
und unendlich vielen, kongruenten n-dimensionalen Kugeln mit gleichem Radius.
Die Kugelmittelpunkte fallen mit den Gitterpunkten zusammen. Außerdem
beschränken wir uns der Einfachheit halber auf Einheitskugeln, was inhaltlich
keine Einschränkung darstellt. Definition: Gegeben seien eine
n-dimensionale, offene Einheitskugel Kn und ein n-dimensionales
Gitter G. Falls je zwei verschiedene Kn disjunkt sind (d.h. sie
schneiden sich nicht) heißt die Menge GP (Kn, G) eine (n-dimensionale)
infinite Kugelgitterpackung. (Beispielabbildungen auf Folie)
Die Packungsdichte infiniter Gitterpackungen
Um herauszufinden, welche Kugelpackungen am dichtsten sind, brauchen wir
zuerst ein Maß für die Dichte einer infiniten Kugelgitterpackung.
Definition: GP (Kn , G) sei eine n-dimensionale infinite
Kugelgitterpackung und F(G) sei das G zugrunde liegende Fundamentalparallelotop,
dann heißt
d (Kn , G) = 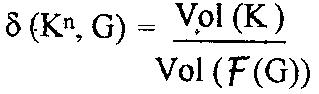
die (infinite) Gitterpackungsdichte der Kugelgitterpackung GP (Kn,
G); 0 < d (Kn , G) <= l.
Die Packungsdichte ist also das Verhältnis von genutztem Volumen (entspricht
z.B. Kreisfläche) zu benutztem Volumen (z.B. des gesamten Fundamentalparallelogramms).
Eine konkrete Rechnung ergibt in der Ebene für die quadratische Packung
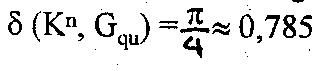
und für die hexagonale Packung
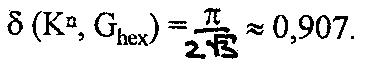
Die hexagonale Kreisgitterpackung bedeckt also 90,7 % der Ebene und ist somit
dichter gepackt als die quadratische, die nur 78,5 % der Fläche bedeckt.
Die dichteste Kreisgitterpackung
Satz (dichteste Kreisgitterpackung, Lagrange 1773): Unter allen Kreisgitterpackungen
besitzt allein diejenige mit hexagonalem Gitter die maximale Packungsdichte 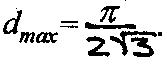
Zum Beweis des Satzes benötigen wir folgendes Lemma:
Lemma: Das Dreieck ABC sei ein Dreieck mit den Seitenlängen a,b,c,
dem Flächeninhalt F und dem Umkreisradius R. Dann gilt: (a) 16F2
= - a4 - b4 - c4 + 2 b2c2
+ 2 c2a2 + 2a2b2 (b) 16 F2R2=
a2 b2 c2
(ohne Beweis)
Beweis des Satzes: G sei ein zweidimensionales Gitter. Wir konstruieren
zu diesem Gitter eine besonders schöne Basis, deren Wert wir erst später
zu schätzen wissen werden. Es sei
B = {(a1,a2) {a1,a2} Basis von G
und |a1| <.| a2 |}
die Menge der längenmäßig geordneten Basen von G und
B1 = { a1| (a1,a2) aus B}
die Menge aller ersten, kürzeren Basisvektoren.
Nun gibt es einen kürzesten ersten Basisvektor c in B1 mit
| c | = min | a1 |
( l )
Zu diesem Vektor c gibt es einen kürzesten zweiten Basisvektor b mit
| b | = min | a2 |
( 2 )
Es ist dann | c | <.| b | und es bildet b zusammen mit c die Basis
{c,b}.Wir können einfach
annehmen, dass der Winkel alpha zwischen c und b spitz ist, weil neben {c,b}
auch {-c,b}, {c,-b} und
{-c,-b} Basen des gleichen Gitters sind. Außerdem gilt für den Differenzvektor
a = c - b ; |a| >= |b|.
Die beiden Basisvektoren c und b und der Vektor a bilden ein Dreieck ABC, dessen
doppelter Flächeninhalt der Fläche des Fundamentalparallelogramms
entspricht.
Für das Dreieck gilt : c <= b <= a .
(3)
Da die gepackten Einheitskreise disjunkt sind (also nicht überlappen) ist
c>2.
Ferner ist nach obigen Überlegungen zur Basis (c,b) der Winkel alpha spitz
: 
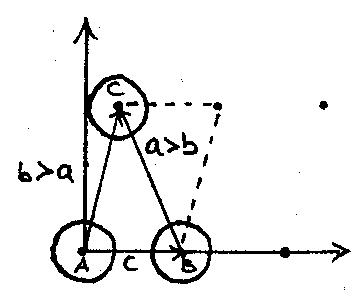
Mit dem Kosinussatz folgt daraus a2<=b2+c2.
(4)
Nach dem Lemma gilt für den Flächeninhalt F des Dreiecks ABC:
16F2 = - a4 - b4 - c4 + 2b2c2
+ 2c2a2 + 2a2b2
= - a4 - b4
+ 2a2b2 +a2c2 - b2c2
- 4c4 +3b2c2 + a2c2
+ 3c4
= (b2
+ c2 - a2) (a2 - b2) + c2
(a2 + 3b2 - 4c2) +3c4 .
Nach
(3) und (4) ist b2 + c2 - a2 >= 0, a2
- b2 >= 0 und a2 + 3b2 - 4c2
>= b2 + 3b2 - 4c2 >= 0.
Also folgt:
16F2>=3c4 , also
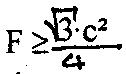
Daher ist das Volumen des Fundamentalparallelogramms mindestens gleich
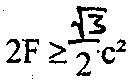 .
.
Gleichheit kann in zwei Fällen auftreten:
1.Fall: b2 +c2
-
a2 = 0 und a2+3b2-4c2
=
0
2. Fall: a2 -
b2 = 0 und a2 + 3b2 - 4c2
= 0
Im l. Fall folgt durch Einsetzen der ersten Gleichung in die zweite
4(b2 - c2) + c2 =0, also b=0, also ein
Widerspruch, da b >= c > 0 ist.
Im 2. Fall ergibt sich a
= b = c. Somit ist das Dreieck ABC gleichseitig, und damit die Packung
hexagonal.
Für c = 2 errechnet man 2F = 2 sqrt(3), woraus
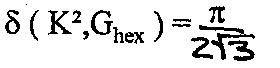
folgt. Insgesamt ist der
Satz damit bewiesen.
Satz
(dichteste infinite Kreisgitterpackung, Thue 1910): Die dichteste Kreispackung
ist die dichteste Kreisgitterpackung und damit hexagonal.
Die dichteste Kugelgitterpackung
Satz über die dichteste Kugelgitterpackung
(C.F. Gauß): Unter allen Kugelgitterpackungen im IR3
besitzt diejenige mit „flächenzentriert-kubischem" Gitter Gfcc
die maximale Packungsdichte dmax = pi / (3 sqrt(2))
Der Satz besagt damit, dass
unter dem Aspekt der dichtesten Kugelgitterpackung das fcc-Gitter das dreidimensionale
Analogon zum hexagonalen Gitter ist. Der Beweis ist deshalb von großer
struktureller Ähnlichkeit zum vorhergehenden. Sein Kernstück
ist wie im zweidimensionalen Fall die Suche nach der kritischen Determinante.
Dazu wird das Volumen des Fundamentalparallelotops bestmöglich zum
Minimum hin abgeschätzt; dies geschieht wieder elementar, ohne Verwendung
der Methoden der mehrdimensionalen Analysis.
Für das Volumen des Fundamentalparallelotops gilt
Vol(F(G))=:2Fd,
Vol(F(G)) 2 =(2Fd)
2 >= 1/2c6.
wobei F den Flächeninhalt des Dreiecks ABC bezeichnet.
Gleichheit gilt in zwei Fällen,
es liegen also zwei verschiedene Minima für Vol (F(G)) vor. Fall (a):
Dieses Minimum wird von der im linken Bild (siehe Folie) skizzierten
Gitterkonfiguration angenommen. Eine Rechnung ergibt |AD| = |BD| = |CD|
= a = b = c . Somit bilden die Punkte A,B,C,D die Ecken eines regulären
Tetraeders. Im fcc-Gitter findet man eine Basis, die ein solches Tetraeder
aufspannt.
Fall (b): Dieses Minimum
wird bei der im rechten Bild (siehe Folie) skizzierten Gitterkonfiguration
angenommen. Eine genaue Rechnung ergibt, dass das Dreieck ABC gleichschenklig-rechtwinklig
ist und, dass |AD| = |BD| = |CD| = b = c. Auch zu diesem Tetraeder findet
man im fcc-Gitter eine Basis, die es aufspannt.
Sowohl in Fall (a) als
auch im Fall (b) liegt also ein fcc-Gitter vor. Für c = 2 errechnet
man das Volumen Vol(F(G)) = 4 sqrt(2) , woraus d ( K3,Gfcc
)
= pi / (3 sqrt(2)) folgt. Damit ist der Satz bewiesen.
Anders
als bei der dichtesten Kreisgitterpackung führen sowohl ein hexagonales
Gitter in der Ebene durch A,B,C (Fall(a)), als auch ein quadratisches Gitter
in dieser Ebene (Fall(b)) zum fcc-Gitter.
Erstaunlich ist hier, dass
es zwei Alternativen gibt und, dass das quadratische Gitter, das in der
Ebene eine vergleichsweise schlechte Kreispackungsdichte erzielt, doch
noch zu einem Raumgitter mit maximaler Packungsdichte ausgebaut werden
kann.
Keplervermutung.
Kepler vermutete, dass die dichteste Kugelpackung gleich der dichtesten
Kugelgitterpackung ist. Dies konnten Hales und Fergusen nun beweisen.
Finite Kugelpackungen
Wir
betrachten zunächst einige wenige Einheitskugeln, die wir möglichst
dicht packen wollen. Für ein und zwei Kugeln ist dies trivial, bei
drei Kugeln muss man die wurstförmige mit der clusterförmigen
Konfiguration vergleichen; ab vier Kugeln hat man sogar die Wahl zwischen
einer Wurst- und mehreren Clusteranordnungen.
Um die Packungsdichte zu
bestimmen benötigen wir zunächst eine Verpackung. Wir beschränken
uns auf Verpackungen, die sich optimal der Packungskonfiguration anpassen
(freie Packung). Den realistischeren, aber schwer systematisierbaren Fall,
dass die Packungskonfiguration einem vorgegebenen Behälter angepasst
werden muss, wollen wir hier nicht weiterverfolgen.
Wir idealisieren: Die Verpackung
ist konvex und selbst volumenlos.
Definition: Sei
K = Kn die offene Einheitskugel im Rn . Wir betrachten
m Kopien K1 , K2 , ... ,Km, die durch
Verschiebung von K entstehen. Dies können wir folgendermaßen
beschreiben: Sei Cm ={c1, c2 ,.. .,cm
} eine Menge von Punkten im Rn. Dann heißt P(Kn,Cm)
eine finite Packung, wenn die gepackten Einheitskugeln disjunkt sind. Eine
finite Packung heißt Wurstpackung, falls alle ci auf einer
Geraden liegen. Sie heißt Clusterpackung, falls sie keine Wurstpackung
ist. Nun ist die Packungskonfiguration umso dichter, je besser sie das
von der Verpackung umschlossene Volumen ausnutzt. Als Packungsdichte bietet
sich somit der Quotient d aus dem von den Kugeln genutzten Volumen zu dem
von der Verpackung benutztem Volumen an. Dann heißt
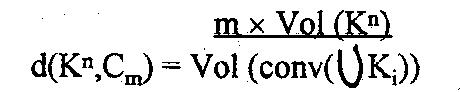 0 < d(Kn,Cm)
<= l
0 < d(Kn,Cm)
<= l
ihre finite Packungsdichte. Dabei bezeichnet conv(X) die konvexe Hülle
der Menge X.
Wurstvermutung und Wurstkatastrophe
Wir betrachten finite Packungen
aus m Einheitskreisen. Dann gibt es für m > 2 immer eine Clusterpackung,
die eine größere Dichte aufweist als die Wurstpackung ("Luftlücken").
Satz: (a) Im
dreidimensionalen Raum gibt es für alle m > 56 außer m = 57,58,63
und 64 Clusterpackungen, die dichter als die Wurstpackung sind.
(b) Im vierdimensionalen
Raum gilt dasselbe für m >= 375370.
In den übrigen Fällen besitzt die Wurst die optimale Packungsdichte,
wobei die Schranken im dreidimensionalen Raum scharf sind, im vierdimensionalen
nicht. Bei scharfen Schranken ändert sich durch Hinzugabe oder Wegnahme
einer einzigen Kugel die optimale Packung sprunghaft von der linearen Anordnung
(Wurst) zum Cluster. Daher heißt diese Vermutung Wurstkatastrophe.
Satz (Wurstvermutung): Wir betrachten finite Packungen
von m Einheitskugeln im Rn. Wenn n > w ist, so ist für
beliebiges m die Packungsdichte der Wurstpackung größer als
die einer jeden Clusterpackung. Man weiß, dass m < 42 ist und
man vermutet, dass w = 5 gilt.
Das Geburtsjahr der Wurstvermutung ist 1975 (L. Fejes Toth); der Beweis
der Wurstvermutung mit w <= 13386 erfolgte 1994 (U. Betke, M. Henk,
J.M. Wills), die Verschärfung w <= 42 erfolgte 1995 (U.
Betke, M. Henk). Eine Aussage in Gestalt der Wurstkatastrophe für
n = 3 und N = 4 galt noch 1975 als hoffnungslos. Sie entstand 1983
und wurde 1985 näher erläutert (J.M. Wills).
(Bilder auf Folie)
Plausibilitätsbetrachtungen
zu beiden Sätzen-
Für alle Wurstkonfigurationen
im Rn lassen sich die Packungsdichten gut berechnen. Der Grenzübergang
„m geht gegen Unendlich“ lässt sich unproblematisch durchführen.
In intuitiver Weise kann man annehmen, dass die maximale Packungsdichte
von Clusterkonfigurationen für „m gegen Unendlich“ gegen die jeweilige
maximale infinite Packungsdichte strebt.
Für kleine m ist im n-dimensionalen Raum (n > 2) die Wurstkonfiguration
gegenüber der Clusterkonfiguration bevorzugt.
Für n = 2 ist der Clusterpackungstyp
für beliebige m bevorzugt.
Für n = 3 ist für kleines m die Wurstpackung bevorzugt, für
großes m die Clusterpackung.
Dazwischen findet die Wurstkatastrophe statt ( m ungefähr gleich
56).
Für n = 4 ist die Situation ähnlich. Jedoch behauptet sich
die Wurst wesentlich länger als im Rn. Der
Übergang zwischen Wurstpackung und Clusterpackung setzt viel später
ein (m ungefähr gleich 375370).
Für n = 5 ist die Wurst für kleine und sehr große
Stückzahlen optimal, also auch für mittlere.
Für n > 5 stabilisiert sich diese Situation.
"Würste":
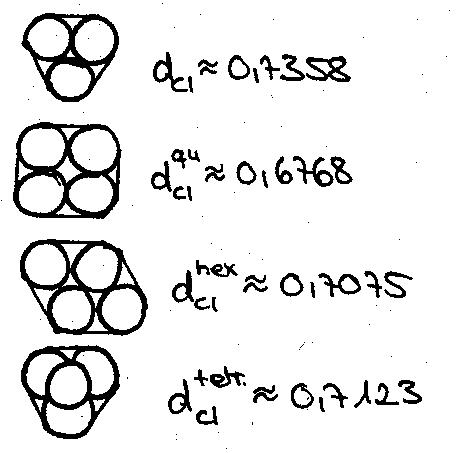
fcc-Gitter:
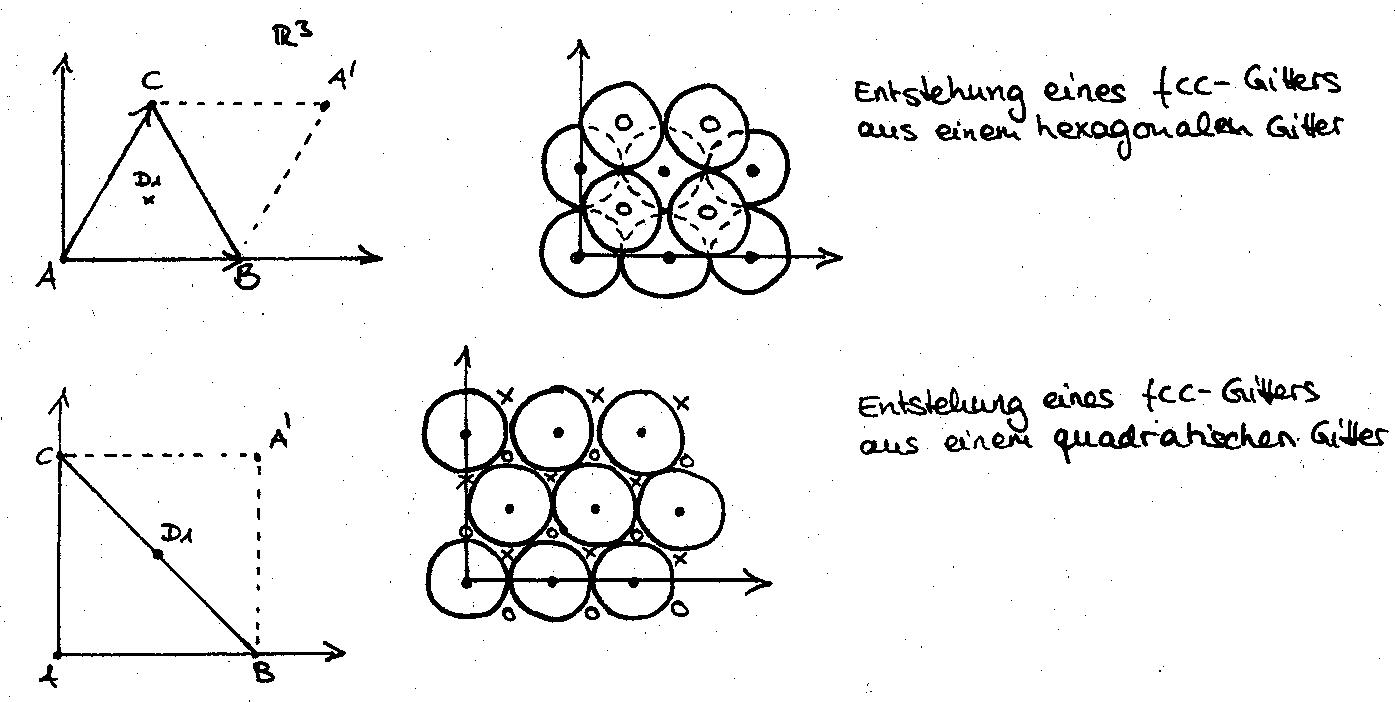
.