Einführung in die Numerik

(Cindy Bönhardt)

Wichtigste Grundprobleme:

Fixpunktprobleme, Lösung von Gleichungen / Gleichungssystemen, Interpolation, Quadratur, Eigenwerte, Approximation, Auswertung von Integralen...
Zur Lösung eines konkreten Problems kann man oft zwischen mehreren Verfahren wählen.

Hintergründe der Verfahren:

Im Gegensatz zur Analysis und linearen Algebra, wo mathematische Probleme exakt behandelt werden, versucht die Numerik, Zahlenwerte als Näherungslösungen zu finden.

Beispiel ( a , b reelle Zahlen, a nicht Null ) :

A * x = b

x = b / a

Die Numerik versucht, effiziente Verfahren mit akzeptablen Aufwand zu finden, mit Beachten des Einflusses des Rundungsfehlers. Das Verfahren muss robust gegen Ungenauigkeiten sein, die sich in Rechnungen dramatisch verstärken können, z.B.:

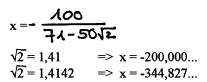
Diese Situation nennt man „schlecht konditioniert".
Bessere Konditionierung durch simple Manipulation:

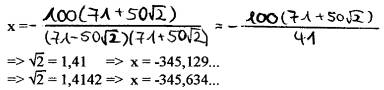
Es muss ein Verfahren gefunden werden, das gut konditioniert ist, um den Einfluss von Fehlern gering zu halten.

Fehleranalyse:

Man unterscheidet:

- Fehler in den Eingabedaten der Rechnung (Messwerte)

- Rundungsfehler

- Abbrechfehler: Viele Methoden liefern selbst bei rundungsfehlerfreier Rechnung die gewünschte Lösung in endlich vielen Schritten zwar beliebig genau, aber nie exakt. Deshalb muss man nach endlich vielen Schritten abbrechen:

Rechenhilfen:

- Analogrechner:

Rechenschieber, Planimeter, elektronische Analogrechner
Zahlen werden durch physikalische Größen (Länge eines Stabes / Größe einer Spannung) ersetzt, das mathematische Problem durch ein physikalisches ersetzt, dessen Lösung in einem Experiment gemessen wird und so indirekt die Lösung ergibt (=> Genauigkeit begrenzt)

- Tischrechenmaschinen / elektronische Digitalrechner:

Größere Genauigkeit erreicht man durch die Gleitpunktdarstellung der Zahlen. Man muss sich merken, an der wievielten Stelle nach der l. Ziffer der Darstellung der Punkt liegt. Die Lage des Punktes wird durch einen Exponenten angegeben:

x= a* 10 ^b , mit | a | < l; b aus IN

also: 30,421 wird dargestellt als 0.30421 * 10²

Exponent b und Mantisse a geben Lage des Dezimalpunktes an. In halblogarithmischer Schreibweise:

0,30421 ₁₀ 2

In jeder Rechenanlage steht aber nur eine endliche feste Anzahl von Dezimalstellen für die Darstellung der Mantisse / des Exponenten zur Verfügung •=> Menge aller Zahlen, die in der Maschine exakt dargestellt werden können, heißt A und ist eine endliche Teilmenge von IR.; ihre Elemente heißen Maschinenzahlen

Wie kann man ein x aus IR, das nicht in A enthalten ist, durch eine Maschinenzahl rd(x) aus A approximieren?

Approximationsproblem: Gesucht ist rd(x) mit: | x - rd(x) | <= | x-g | , für alle g aus A

So ein rd(x) erhält man durch Rundung:

rd(3,14159 ₁₀ 0) =0,3142 ₁₀ l
rd( 0,142842 ₁₀ 2) = 0,1428 ₁₀ 2

Maschinengenauigkeit:

Geg.: Maschine mit t - Dezimalstellen
Ges.: rd(x)

Dezimaldarstellung von | a | sei:

Dann bildet man:

d.h. man erhöht a um l, falls die (t+1)-te Ziffer a >= 5 ist, und man schneidet nach der t- ten Ziffer ab. Schließlich setzt man

Relativer Fehler von rd(x):

Algorithmus:

Wir wissen: a+b+c = (a+b)+c = a+(b+c)

Dies kann aber bei der Gleitpunktdarstellung zu unterschiedlichen Resultaten führen. Deshalb ist es aus numerischen Gründen wichtig, genau zwischen verschiedenen mathematischen äquivalenten Formulierungen einer Rechenmethode zu unterscheiden: Als Algorithmus bezeichnet man eine der Reihenfolge nach eindeutig festgelegte Sequenz von endlich vielen „elementaren Operationen“, die vorschreibt, wie aus gewissen Eingabedaten die Lösung eines Problems berechnet werden soll.
Ein Algorithmus ist eine eindeutige Rechenvorschrift zur Berechnung von realen Funktionen, denn das Problem besteht darin, aus gewissen Zahlen x₁, ..., x_n endlich viele Resultatdaten y₁, ..., y_n zu berechnen.
Unterschiedliche Resultate erhält man wegen der Fortpflanzung des Rundungsfehlers. Dies ist das wichtigste Kriterium für die Beurteilung der „Güte" eines Algorithmus.

Interpolation:

Gegeben ist eine Funktion

,

die von n + l Parametern (auch: Basisvektoren) a₀, ..., a_n abhängt. Ein Interpolationsproblem für liegt dann vor, wenn die Parameter a₀, ..., a_n so bestimmt werden sollen, dass für n + l gegebene Paare von reellen oder komplexen Zahlen ( x_i , f_i.); i = 0, ..., n ; x_i ungleich x_k für i ungleich k, gilt:

Die Paare ( x_i , f_i.) werden als Stützpunkte bezeichnet. Ein lineares Interpolationsproblem liegt vor, wenn linear von den Parametern abhängt:

Dazu gehört das Problem der Interpolation durch Polynome:

und der trigonometrischen Interpolation:

Früher wurde Polynominterpolation verwendet, um Formeln für die numerische Integration von Funktionen abzuleiten. Nun benutzt man sie zur Gewinnung von Algorithmen, um die Konvergenz gewisser Folgen zu beschleunigen. Trigonometrische Interpolation dient der numerischen Fourieranalyse von Messreihen. „Spline-Interpolation“ gehört auch zu den linearen Interpolationsproblemen, bei der Funktionen benutzt werden, die

1. 2mal stetig differenzierbar sind für x aus [x₀ ; x_n ]

2. in jedem Teilintervall [x_i ; x_i+1 ] mit einem Polynom 3. Grades übereinstimmen
Dabei ist vorausgesetzt, dass die Interpolationsabszissen x_i , i = 0,....n reelle Zahlen sind mit x₀ < x₁ < ... < x_n . Sie wird verwendet zur zeichnerischen Darstellung von Kurven, die „möglichst glatt“ durch vorgegebene Punkte ( x_i , f_i.) gehen sollen. Zu nichtlinearen Interpolationsproblemen gehören die Interpolation durch rationale Funktionen:

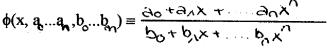
und durch Expotentialsummen:

Rationale Interpolation verwendet man für konvergenzbeschleunigende Algorithmen. Die Expotentialsummen - Interpolation ist wichtig für die Analyse von Zerfallsreihen in der Physik und der Chemie.

Beispiel für Polynominterpolation:
Interpolationsformel von Lagrange:

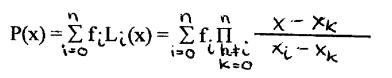
Diese Formel zeigt, dass P linear von den Stützwerten f_i. abhängt. Für praktische Rechnungen weniger geeignet, falls n größere Zahlen annimmt.

Beispiel: n = 2
Geg.:

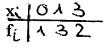
Ges.: P(2)

Lösung:

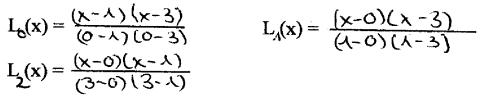
P(2) = l * L₀ (2) + 3 * L₁ (2) + 2 * L₂ (2) = l * (-1/3) +3*1+2*1/3 = 10/3

Numerische Integration:

Unter numerischer Integration versteht man die approximative Auswertung von Integralen, besonders
vom Typ:

Wobei im zweiten Fall R ein mehrdimensionaler Bereich und entsprechend x ein Vektor und dx Abkürzung für dx₁ , dx₂., ... ist.

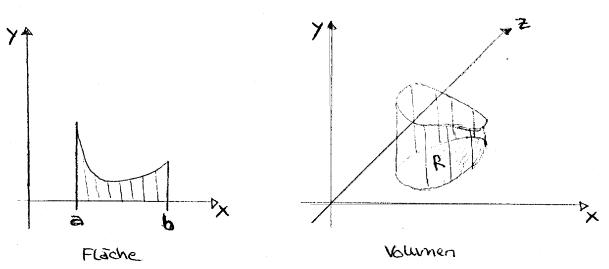
Integration braucht man, weil auch bei einfachen Funktionen das Integral nicht zu berechnen ist, da man die Stammfunktion nicht aufsuchen kann, z.B. f(x) = l / ( xe^x ) oder f(x) = sin (x/ sqrt(x)) Oft ist auch f in geschlossener Form nicht bekannt, weil f durch Messungen ermittelt wurde, z. B. wenn man die Durchflussmenge M pro Zeiteinheit eines Flusses an einer bestimmten Stelle ermitteln will, so wird der Flussquerschnitt Q mit Hilfe von Messungen ermittelt.

Allgemein erhält man für alle natürlichen Zahlen n zur näherungsweisen Berechnung von Integrationsformeln der Art

die sogenannten Newton-Cotes-Formeln. Die „Gewichte" a_i , i = 0,1,...n liegen tabelliert vor. Es sind rationale Zahlen mit der Eigenschaft

Dabei bleibt aber ein Approximationsfehler erhalten.

Approximation:

Problem: f(x) = x⁵ + x³ – 10^-20 = 0

Die Lösung muss 0 < x* << l erfüllen, so dass man x⁵ gegenüber x³ vernachlässigen kann.

Angenäherte Gleichung: x³ = 10^-20

Erste grobe Abschätzung: x*=10^{-20 / 3} = 2,5* 10^-7

Genauerer Weg: Newton - Verfahren

Konstruktion einer konvergenten Zahlenfolge, deren Grenzwert die Lösung ist.
Voraussetzungen:

f: IR -> IR stetig differenzierbar
x* Lösung für f(x) = 0

f(x*) ungleich 0

Dann existiert eine Umgebung U(x*) von x*, so dass die rekursiv definierte Folge

(iteratives Verfahren)

für jeden Startwert x aus U(x*) gegen die Lösung x* geht.
Wahl für Beispiel von oben, in der Nähe der Lösung, also etwa x = 0,3

=> x₀ = 0,3

x₁ = 0,2052
x₁₀ = 5,496* 10
x₄₀ = 2,154* 10

Die einzige Frage ist, wann man aufhört zu iterieren, und wie groß der verbleibende Fehler | x - x* | ist.