Routenplanung

(Leonard Osang)

1. Allgemeines:

Unter Routenplanung versteht man die Suche nach der optimalen Verbindung mehrer Orte bzw. Punkte. Dabei spielen verschiedene Faktoren eine Rolle:

- Sucht man eine Verbindung mit kürzestem Weg oder mit kürzestem Zeitaufwand?

- Welche Parameter muss man berücksichtigen (z.B. im Straßenverkehr: Staus, Verkehrsbehinderungen) ?
Es gibt verschiedene Anwendungsbereiche:

- Reiseroutenplanung

- Optimale Routen für öffentliche Verkehrsmittel (z.B. Bus)

- Optimale Routen für Müllabfuhr, Post

- Mobilfunk, Satellitenübertragung (Berechnung bestmöglicher Standorte für Serverknotenpunkte)

- Mikroelektronikindustrie (Leiterplatinen, Mikroprozessorenarchitektur)

2. Der Graph als geeignetes Hilfsmittel:

Graph G = (V,E)

G besteht aus

V, einer endlichen Menge von Knoten, sowie aus

E, einer Menge 2-elementiger Teilmengen von V, den Kanten

Knoten können Haltestellen im öffentlichen Verkehrsbetrieb, Autobahnkreuze auf dem Stadtplan, oder auch Bohrlöcher auf einer Leiterplatine darstellen, je nach Bedarf.

Kanten sind die Verbindungsstücke zwischen den Knoten. Wenn eine Verbindung nur in eine Richtung gilt, spricht man von Bögen, eine Art Einbahnstraße. Solche Bögen werden mit Pfeilen markiert.

Diese Kanten bzw. Bögen besitzen meistens sogenannte Gewichte. Sie können für Fahrzeiten, Gehminuten oder Distanzen stehen. Sie können positiv, als auch negativ sein.

Beispiel Multigraph:

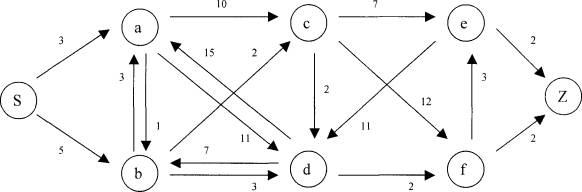
Optimale Weglänge: 11

Zur Lösung solcher Probleme auf einem mathematischen Weg wurden spezielle Algorithmen entwickelt, die auch für Computer verständlich sind.
Zum Beispiel der Dijkstra Algorithmus:

Vom Startpunkt aus werden die Alternativen schrittweise durchgerechnet, also vom Punkt S zum Punkt a und b. Dann von a und b zu allen nächstmöglichen Zielen, hier c und d. Falls man einen Punkt durch mehrere Wege erreicht, wird der kürzere gewählt.
Dieser Vorgang wird wiederholt, bis S in Z liegt. Route und Distanz werden berechnet. Dieses Verfahren kann nur auf Graphen mit ausschließlich positiven Bogengewichten angewandt werden.

Dieser Algorithmus ist sehr gut geeignet für Bordcomputer oder andere Navigationssysteme, da in diesem Vorgang nach jeder Kantenfahrt alle Alternativen erneut geprüft werden. So können Veränderungen im Kantennetz (bzw. Straßennetz), wie Stauentwicklung oder Unfälle, sofort berücksichtigt werden.
Der Kruskal-Algorithmus erstellt in kürzester Zeit einen Spannbaum, d.h. ein Netz, das alle Knoten in einem Graphen optimal verbindet. Sehr hilfreich für die Planung von Netzwerken aller Art über größere Entfernungen.

3. Das Chinesische-Postboten-Problem:

Angenommen, eine Müllabfuhr muss ihre Runde drehen. Jede Straße (Kante) muss einmal abgefahren werden:

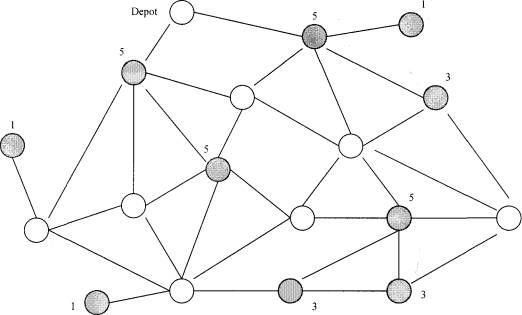
Hier muss ein Eulerscher Kreis (auch Eulerweg: gemeint ist ein Weg, auf dem man jede Kante genau einmal befährt) erstellt werden. Für den Graph oben bedeutet das, dass man zuerst einmal zusätzliche Kanten einbauen muss (vollständiger Graph, siehe unten).

Satz von Euler:

Für jeden bis auf isolierte Knoten zusammenhängenden Graphen G = (V,E) gilt:

a) Es existiert genau dann ein Eulerweg in G, wenn höchstens zwei Knoten in V ungeraden Grad besitzen

b) Es existiert genau dann ein Eulerkreis in G, wenn alle Knoten in V geraden Grad haben

Die Punkte mit ungerader Gradzahl müssen also öfters besucht werden. Dazu muss die Müllabfuhr Sonderfahrten machen, also manche Kanten öfters abfahren. Es ergeben sich folgende Sonderfahrten (rot)

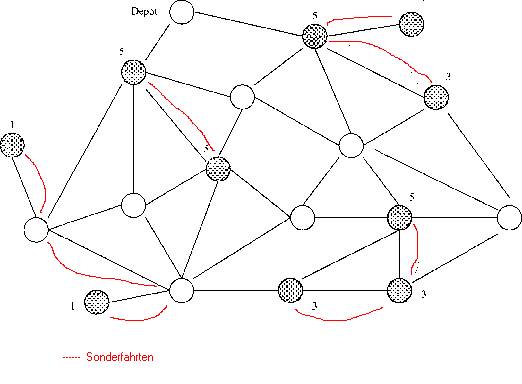
Algorithmus zum Chinesischen-Postboten-Problem

Input: Gewichteter Graph G = (V,E)
Output: Geschlossener Weg minimaler Länge, der jede Kante von G enthält

1. Bestimme die Menge V' der Knoten ungeraden Grads in G

2. Bestimme die Länge der kürzesten Wege zwischen je zwei Knoten aus V

3. Bestimme ein bezüglich dieser Abstände optimales Matching M im vollständigen Graphen G' auf den Knoten in V’

4. Konstruiere aus G und den zu den Kanten des Matchings M gehörenden Wegen von G den Multigraphen G"

5. Bestimme einen Eulerkreis in G "

4. Das „Traveling-Salesman-Problem“

Das „TSP“ ist eines der berühmtesten graphentheoretischen Probleme. Man versucht, eine kürzeste Rundreise durch verschiedene Orte (Knoten) zu finden. Für dieses Problem gibt es leider keinen festen Algorithmus. Man behilft sich mit Annäherungen an die Optimalroute (bei 10 Knoten gibt es bereits mögliche 181.440 Rundreisen). Durch Kombinatorische Optimierung, ein ganzes Teilgebiet der Mathematik, gelang es George Dantzig im Jahr 1954, ein Rundreiseproblem mit 49 Städten zu lösen. Auf seine damaligen Methoden greifen noch heute Wissenschaftler zurück. Er nutzte das so genannte Branching-Verfahren.

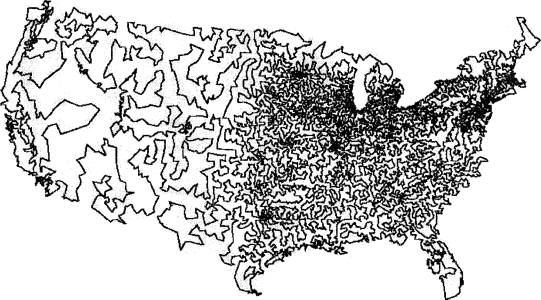
Rundreise durch alle Orte der USA mit 13.509 Knoten

Rundreise durch Deutschland mit 15.112 Knoten (momentaner Weltrekord)

Plan für Bohrlöcher in einer Leiterplatine mit optimaler Route

Quellen:

- Das Geheimnis des kürzesten Weges, Peter Gritzmann, Rene Brandenberg, Springer Verlag

- www-m9.ma.tum.de
- www.math.princeton.edu/tsp